- Importance Sampling
- Catene di Markov
- Schema del metodo Metropolis Monte Carlo
- Punti salienti di un programma MC
- Calcolo di
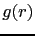
Giorgio F. Signorini
Date: 2007-2008
(basato su ())
Cerchiamo il valore di aspettazione di una funzione ![]() distribuita
secondo una probabilità
distribuita
secondo una probabilità ![]() sul dominio delle
sul dominio delle ![]() :
:
![$\displaystyle E\left[g(x)\vert p\right]=\int g(x)p(x)dx$](img4.png)
(assumiamo
![\includegraphics[scale=0.6]{funzioni}](img51.png)
Una stima empirica di ![]() , generando
, generando
![]() secondo
secondo
![]() , è
, è
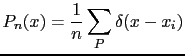
La corrispondente stima empirica di ![]() è
è
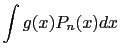 |
|||
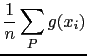 |
Se però non siamo in grado di generare punti secondo ![]() , ma secondo
un'altra distribuzione
, ma secondo
un'altra distribuzione ![]() (nel caso banale, una distribuzione uniforme),
si può scrivere il valore di aspettazione come
(nel caso banale, una distribuzione uniforme),
si può scrivere il valore di aspettazione come
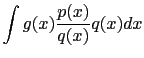 |
|||
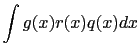 |
|||
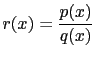
La stima empirica su ![]() del valore di aspettazione di
del valore di aspettazione di ![]() è
è
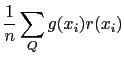 |
Quanto è accurata una certa stima di ![]() fatta con
fatta con ![]() punti? Cioè,
quanto si discosta
punti? Cioè,
quanto si discosta ![]() dal valore vero
dal valore vero ![]() ? Dipende da
? Dipende da ![]() ma anche dalle proprietà di
ma anche dalle proprietà di ![]() e di
e di ![]() (o
(o ![]() ). Ad esempio,
se
). Ad esempio,
se
![]() , il valore di aspettazione stimato con qualunque
, il valore di aspettazione stimato con qualunque
![]() è
è ![]() , e l'errore è nullo per qualunque
, e l'errore è nullo per qualunque ![]() . Negli altri casi,
a parità di
. Negli altri casi,
a parità di ![]() , possiamo aspettarci che sarà tanto minore quanto
minore è la variazione di
, possiamo aspettarci che sarà tanto minore quanto
minore è la variazione di ![]() in un campionamento secondo
in un campionamento secondo ![]() .
.
L'accuratezza della stima è misurata dalla varianza della media
![]() (da non confondere con la varianza dei dati,
(da non confondere con la varianza dei dati,
![]() ).
).
L'equazione (![]() ) conferma che a parità di
) conferma che a parità di ![]() l'errore sulla stima è dato dalla variazione quadratica della
l'errore sulla stima è dato dalla variazione quadratica della ![]() ,
e che se
,
e che se ![]() allora
allora ![]() .
.
Se invece che su ![]() , campioniamo su
, campioniamo su ![]() , l'errore sulla stima è
, l'errore sulla stima è
L'equazione (![]() ) corrisponde esattamente alla (3.1.9)
in (), con
) corrisponde esattamente alla (3.1.9)
in (), con
![]() e
e ![]() .
.
Consideriamo due casi limite:
Il confronto tra quest'ultima equazione e la (![]() )
ci dice che la differenza tra fare una stima del valore di aspettazione
di
)
ci dice che la differenza tra fare una stima del valore di aspettazione
di ![]() campionando
campionando ![]() in modo uniforme e campionandola secondo
la sua distribuzione
in modo uniforme e campionandola secondo
la sua distribuzione ![]() è data dalla differenza nella variazione
quadratica di
è data dalla differenza nella variazione
quadratica di ![]() e di
e di ![]() rispettivamente. Se
rispettivamente. Se ![]() è molto ``piccata'' (come è la distribuzione nell'insieme canonico)
la differenza può essere enorme. Se al contrario il prodotto
è molto ``piccata'' (come è la distribuzione nell'insieme canonico)
la differenza può essere enorme. Se al contrario il prodotto ![]() varia meno di
varia meno di ![]() , cioè
, cioè ![]() varia molto proprio dove
varia molto proprio dove ![]() è bassa,
l'errore nella stima può essere più basso se la stima viene calcolata
con campionatura uniforme.
è bassa,
l'errore nella stima può essere più basso se la stima viene calcolata
con campionatura uniforme.
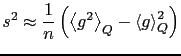
Si immagina1.1 di fare
![]() stime ciascuna basata su
stime ciascuna basata su ![]() punti:
punti:
![]() ,
,
![]() ,
, ![]() , e di fare la varianza di
queste stime:
, e di fare la varianza di
queste stime:
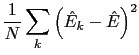 |
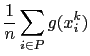 |
|||
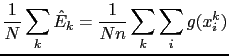 |
Con notazione sintetica (
![]() e
e
![]() )
si ha:
)
si ha:
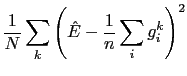 |
|||
![$\displaystyle \frac{1}{N}\sum_{k}\left(\frac{1}{n}\sum_{i}\left[g_{i}^{k}-\hat{E}\right]\right)^{2}$](img65.png) |
|||
![$\displaystyle \frac{1}{N}\sum_{k}\frac{1}{n^{2}}\left(\sum_{i}\left[g_{i}^{k}-\hat{E}\right]\right)\left(\sum_{j}\left[g_{j}^{k}-\hat{E}\right]\right)$](img66.png) |
se i punti ![]() sono estratti in maniera casuale sul dominio
sono estratti in maniera casuale sul dominio ![]() ,
i termini misti si annullano:
,
i termini misti si annullano:
![$\displaystyle \frac{1}{N}\sum_{k}\frac{1}{n^{2}}\sum_{i}\left[g_{i}^{k}-\hat{E}\right]^{2}$](img68.png) |
|||
![$\displaystyle \frac{1}{n}\frac{1}{N}\sum_{k}\frac{1}{n}\sum_{i}\left[\left(g_{i}^{k}\right)^{2}-\hat{E}^{2}\right]$](img69.png) |
|||
![$\displaystyle \frac{1}{n}\left[\left\langle g^{2}\right\rangle _{P}-\left\langle g\right\rangle _{P}^{2}\right]$](img70.png) |
|||
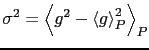
In sostanza, nel limite
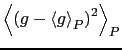 |
|||
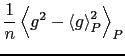 |
|||
(basato su ())
Il problema è generare punti con una distribuzione di probabilità che approssimi la distribuzione canonica.
In una catena di Markov
![$\displaystyle \rho^{(2)}\pi=\left[\rho^{(1)}\pi\right]\pi$](img81.png) |
|||
La catena ammette un limite
tale che
Dall'ultima equazione si capisce che lo stato limite ![]() esiste
se
esiste
se ![]() ammette autovalore
ammette autovalore ![]() . Se il numero di stati è finito,
lo è anche il numero di vettori
. Se il numero di stati è finito,
lo è anche il numero di vettori
![]() . (approfondire:
come si può essere sicuri che si arriva comunque al limite
. (approfondire:
come si può essere sicuri che si arriva comunque al limite ![]() ?)
?)
Nell'esempio del sistema a due stati (il calolatore), si suppone che
![]() sia nota.
sia nota.
Nelle simulazioni MC, si conosce ![]() (ogni elemento
(ogni elemento
![]() ),
e si vuole trovare
),
e si vuole trovare ![]() .
.
Vi sono varie possibili soluzioni.
Si può porre la condizione (non necessaria) della reversibilità microscopica:
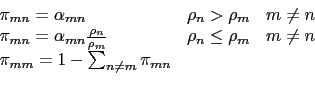
N.B. che questa variazione è
![]() ,
e se la mossa viene accettata, va aggiornata sia la
,
e se la mossa viene accettata, va aggiornata sia la ![]() che tutte
le altre
che tutte
le altre
![]() , di una quantità
, di una quantità
![]() In sostanza si deve conservare in memoria ogni singola interazione
In sostanza si deve conservare in memoria ogni singola interazione
![]() .
.
In pratica il ![]() si calcola come:
si calcola come:
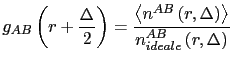
cioè il rapporto tra il numero medio di particelle B a distanza da una particella A compresa tra
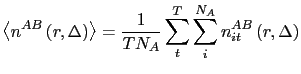
e lo stesso in un sistema ideale
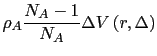 |
Quindi:
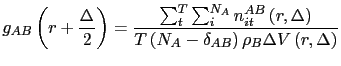
Note pratiche: